In a StreamBase application you may want to know when tuples are available for analysis in a specific sequence. Examples of problems where pattern matching can be useful:
-
Lost customers: someone added an item to a shopping cart, but has not checked out within a certain time
-
Potential break-in attempts: failed logins using multiple user ids during a single session
-
Timeout during sensitive operations such as password resets
-
Financial fraud: inbound and outbound money transfers over a certain amount; or for the same amount within a certain time
Using the StreamBase pattern language, you can apply pattern queries to events enqueued on one or more input streams. Pattern queries can be described as containing at least three parts:
- Template
-
Identifies one or more named streams (or subqueries that evaluate to stream names), and selects data from the streams that matches a specified pattern.
- Window
-
Provides a terminating event for the query, since the streams themselves may be unlimited. Windows must be bounded by either elapsed time (for example, all tuples received over one day), or by a range of values in a specified field.
- Predicate (optional)
-
Filters the potential result of the query template. A predicate pattern is expressed as a WHERE clause.
- Output schema
-
Specifies how the data resulting from the template selection and predicate should be included in the output tuple, which is released when the window closes.
To perform pattern queries, continue with these topics:
-
For EventFlow applications: Using the Pattern Operator
After adding a Pattern operator to your application flow, you will edit the operator's Properties view to specify the desired template and interval values. A predicate containing a WHERE clause allows additional tuning of the match pattern.
-
For StreamSQL applications: SELECT Statement
Use the FROM PATTERN clause to specify the template and interval, and the WHERE clause for adding constraints.
-
For both types of applications: StreamBase Pattern Matching Language
Describes the syntax of pattern expressions.
This rest of this topic illustrates how to use pattern matching by providing some brief application examples.
It is appropriate to discuss pattern matching on a single stream and matching across multiple streams as separate topics.
Pattern matching on a single stream is only really useful if you include a predicate that is satisfied by the events happening
in a particular order. When you want to detect patterns within tuples, or events arriving on a single stream, you can use
aliasing to indicate how many events are included in the template. For example, if you want to consider pairs of events, the
template will reference the same stream twice applying a different alias to each reference. The following StreamSQL template
indicates that the pattern involves two events arriving in a specified order on the stream named InputStream:
InputStream AS stream1
THEN InputStream AS stream2For patterns involving a greater number of events, the template becomes more complex. This StreamSQL template describes a pattern involving three events:
(InputStream AS s1 AND InputStream AS s2)
THEN InputStream AS s3Note how parentheses are used to specify the pattern; the AND operator indicates that the order of the first two events is not specified, but both of these events must occur before the third event, which follows the THEN operator.
To complete either of these pattern specifications, you must specify the period of time within which the pattern must be detected and apply constraints that would further limit the events that satisfy the pattern. Without these additional entries, the template itself has little meaning.
Let's more fully flush out the details of an example, first using StreamSQL and then an EventFlow diagram.
CREATE INPUT STREAM InputStream
(stock string, price double, shares int);
CREATE OUTPUT STREAM Out AS
SELECT s1.stock AS stock1, s1.price AS price1,
s1.shares AS shares1, s2.shares AS shares2
FROM PATTERN InputStream AS s1 THEN
InputStream AS s2 THEN
InputStream AS s3
WITHIN 20 TIME
WHERE s1.stock=s2.stock AND s2.stock=s3.stock AND
((s3.price>s2.price) OR (s3.price>s1.price));A single input stream is referenced three times in the FROM PATTERN clause; consequently, each stream must later be referred to through its alias named. The WITHIN clause specifies that the desired pattern be detected within 20 seconds; fractional seconds, for example, 20.5, are also acceptable. Finally, the WHERE clause specifies that the pattern involves three events with identical values in the stock field, where the value in the price field of the third event is greater than the price field in either the first or second event. The target list following the SELECT keyword lists the field values that will be included in the tuple emitted by this statement when a successful pattern match has been identified.
The following EventFlow application produces the same result.
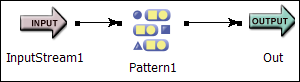 |
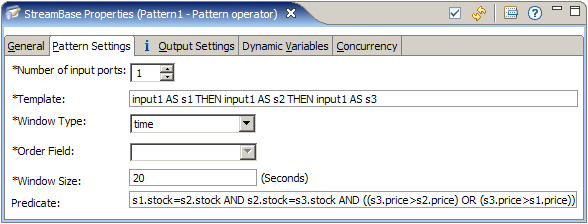
Two tabs within the Pattern operator's StreamBase Properties view are used to configure this operator. On the Pattern Settings tab, enter the template, size value, and predicate (which correspond to the FROM PATTERN, WITHIN, and WHERE clauses in the StreamSQL statement).
 |
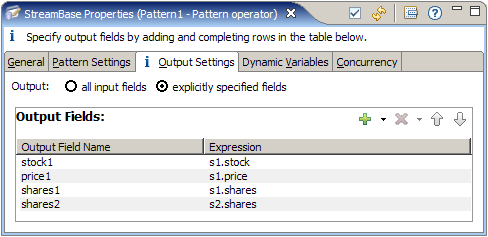
On the Output Settings tab specify the fields that will be included in the emitted tuple. Since an arc in an EventFlow application
does not have a name, in the following figures the incoming stream is referred to using a name derived from its corresponding
input port. The single input port in this example is named input1.
 |
Start either version of this application and then enqueue the following tuples. (You must submit all of the tuples within the specified time period. If you are uncomfortable with this constraint, increase the value.)
After enqueuing the third tuple, nothing was emitted on the output stream. This is correct as s3.price was not greater than the price value in either of the first two tuples.
After enqueuing the fourth tuple, three tuples are emitted.
Data dequeued from the sample application
|
stock1 |
price1 |
shares1 |
shares2 |
|
a |
22.0 |
1 |
2 |
|
a |
22.0 |
1 |
3 |
|
a |
23.0 |
2 |
3 |
Since all the tuples were enqueued during the specified time duration, the first emitted tuple results from the first, second and fourth tuples satisfying the pattern and the second emitted tuple results from the first, third and fourth tuples satisfying the pattern. Finally, the third tuple results from the second, third and fourth tuples satisfying the pattern.
As a further example, you should enqueue the following eight tuples.
Data enqueued to the sample application
|
stock |
price |
shares |
|
a |
22.0 |
1 |
|
a |
23.0 |
2 |
|
a |
21.0 |
3 |
|
a |
21.0 |
4 |
|
a |
21.0 |
5 |
|
a |
21.0 |
6 |
|
a |
21.0 |
7 |
|
a |
25.0 |
8 |
If you work quickly enough so that all eight tuples are enqueued within the specified time duration, no tuples are emitted until the eighth tuple is enqueued. Then, 21 tuples are emitted. Review the values in the shares1 and shares2 fields, which illustrates that multiple matching patterns have been detected.
Now, investigate the effect of changing the value of the stock field in some of the tuples. Just make sure you enqueue at least three tuples with the same stock field value, and make sure the price field in the third tuple is greater than the price field values in either the first or second tuple.
Setting up a pattern matching specification that involves multiple streams is similar to the single stream variant with the exception that it is no longer necessary to provide an alias name for each distinct stream. Of course, if the pattern involves multiple events on one of the streams, then the multiple references to this stream will need to be aliased.
The following StreamSQL application detects a pattern across the tuples enqueued onto two separate input streams.
CREATE INPUT STREAM InputStream1 (
stock string,
value double
);
CREATE INPUT STREAM InputStream2 (
stock string,
value double
);
CREATE OUTPUT STREAM Out;
SELECT InputStream1.stock AS stock,
InputStream1.value AS value1,
InputStream2.value AS value2
FROM PATTERN (InputStream1 THEN InputStream2) WITHIN 20 TIME
WHERE (InputStream2.value > InputStream1.value) AND
(InputStream1.stock = InputStream2.stock)
INTO Out;Notice how it is unnecessary to provide an alias name for each distinct stream.
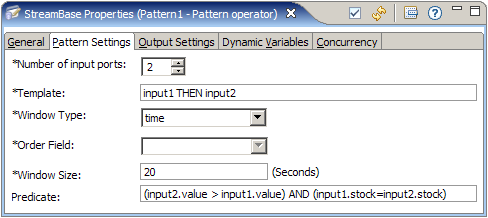
The equivalent EventFlow application is described in the following figures.
 |
 |
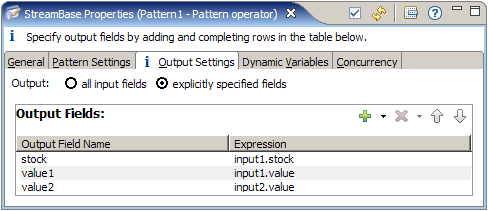 |
Notice that each incoming arc is referenced through its associated input port.
